黑洞數位全息圖

早在 1970 年代後期（我所知最早的研究）^[1]就已經有了黑洞視覺化的工作；到了 2014 年，《星際效應》以壯觀且大體上符合科學的「Gargantua」黑洞視效，將黑洞視覺化推向大眾。互聯網上也充斥各式各樣的黑洞模擬與圖像。因此，一個合理的疑問是：既然已有如此海量相關內容，為什麼還要繼續製作新的視覺化作品呢？

對我而言，答案在於：即使是《星際效應》那樣的視覺化，也尚未達到全息圖所能呈現的「逼真度」。即便只是單純的立體 3D（stereo 3D），就已能大幅提升真實感，但市面上的黑洞視覺化連這一點都幾乎沒實現（當然先決條件是，黑洞本身在理論上就不會「破壞」立體 3D，我們稍後會再提及）。若能運用高品質的全視差數位全息（full-parallax digital holography），其逼真程度會比單純的立體 3D更高；但目前大多數現有的黑洞視覺化卻連後者都尚未達成。

有些全彩全息圖實在逼真到讓人無法輕易分辨自己究竟看到的是實體物還是全息影像。^[2] 例如，Philippe Gentet 曾在首爾的實驗室中向我展示過一件作品：同一個箱子中，一個是真品，一個是記錄在玻璃表面的全息影像。他要我猜哪個是真實物體。我毫無頭緒，直到他轉動了某個旋鈕，使其中一個模型變暗，我才立即斷定變暗的必定是全息圖——結果卻猜錯了。

我並不是要宣稱我所做的黑洞全息圖已經達到以上那般的逼真程度；只是想說，數位全息或許是視覺化黑洞的「最佳媒介」，值得一試。

與 3D 阿波羅尼安墜道（Apollonian Gasket）不同的是，做黑洞的時候，我不能像以前那樣「不太需要懂數位全息的原理」。當初我可以直接使用 Chimera Holography 編寫給 3D Studio Max 的腳本與影像轉製流程，等同於將整個處理過程視為黑箱即可。然而，想要將黑洞載入 3D Studio Max 幾乎不可能；你需要自行編寫一個繪圖引擎，並且和 Chimera 的腳本進行整合。此外，後面也會提到，因為黑洞牽涉到「彎曲光線」的問題，如果想要將它做成全息圖，某些演算法也需要調整。

在開始這個黑洞專案時，我甚至不確定黑洞的立體 3D 影像是否「可行」。如同我前面暗示的，黑洞可能使得視覺變得過於扭曲，我們的大腦無法正常理解——而網路上也幾乎找不到「黑洞立體圖」，也許就是因為這緣故。有篇論文^[3]也提出類似的推測。於是，我先嘗試做了黑洞的立體對（stereo pair）；如果連這都失敗了，那麼做全息圖就更無望了。

黑洞之所以可見，主要是因為它會彎曲光線。在一般的光柵式渲染器（例如 Blender 或 3D Studio Max）中，並無法直接呈現黑洞；你需要用「光線追蹤（ray tracing）」，而且必須改寫它的部分，讓光線依照黑洞的測地線軌跡進行——也就是「非線性光線追蹤（nonlinear ray tracing）」，如下圖所示。我這裡不細談演算法細節，只簡單提及這其實是幾十年前就被研究得相當透徹的技術，一個高中的優秀生都能自己實作（如果足夠努力），並留下參考文獻^[4]。

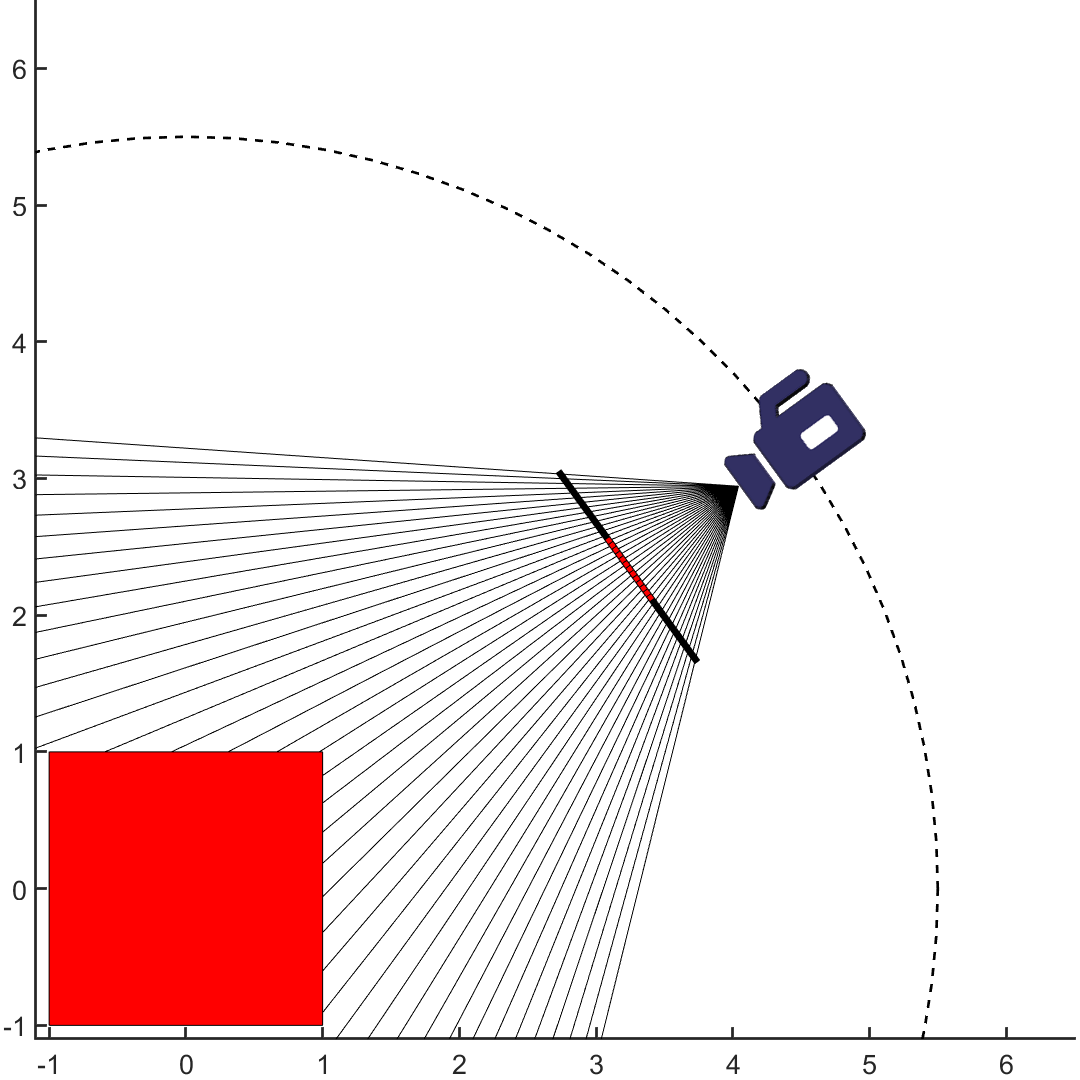
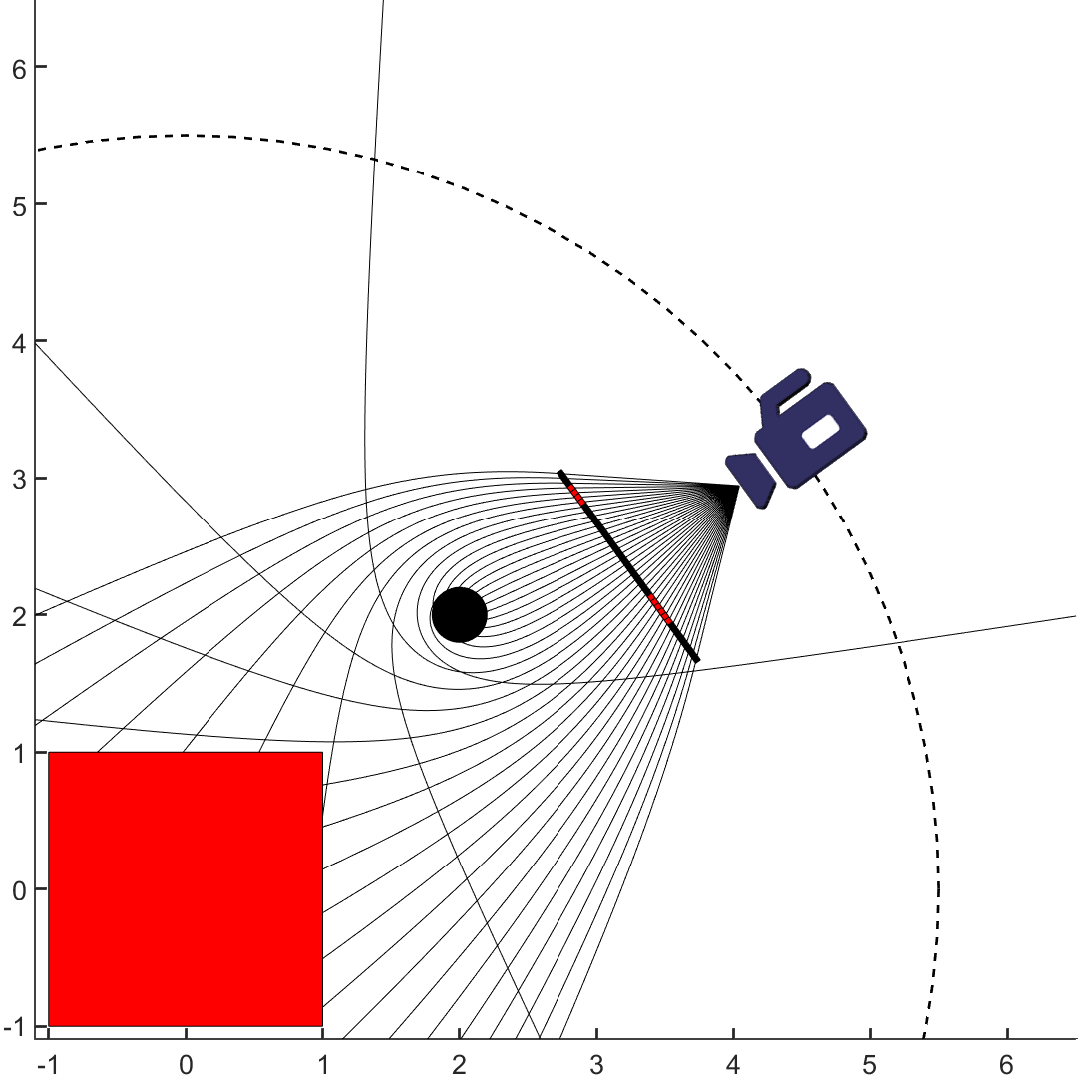
大學時我就做了一套光線追蹤程式，並持續維護到現在。先前我給它添加了黑洞功能，但僅限於假設「環境在無窮遠處」的情況；為了做出有趣的立體對（stereo pair），必須讓環境處在黑洞的有限距離範圍內，所以我對程式做了相應修改。起初，我設計了「黑洞懸浮在無邊海洋之上、周圍有炙熱的吸積盤與極光背景」的場景（如下兩張圖）。令人欣慰的是，立體效果確實可行。想要測試立體效果的話，可以試著用交叉眼（cross-eye）的方法觀看（可參考 這段教學）。若成功，你會感覺黑洞像個玻璃球，而它身後的天空則彷彿向螺旋深處彎曲。

這代表只要在原理上可行，就能把黑洞做成全息圖。然而，當時我也已經學了 Jacques Desbiens 的數位全息課程，得知我原本的場景配置不太合適。原因在於數位全息圖存在「全息景深（holographic depth of field）」的限制：在反射式數位全息（reflection hologram）的情況下，只有在全息平面上、或距該平面距離相對小範圍內的物體才會清晰，超出範圍就容易失焦。簡單來說，若你製作的全息圖寬度為 w、高度為 h，那麼物體最好不要離該全息平面超過 max(w,h) 的三分之一（前方）或三分之二（後方）。

鑑於這一點，我不能再用「無邊海洋」的概念，只好把海洋「封閉」成一個地下水池，靈感部分來自我若干年前去過的伊斯坦堡地下水宮（Basilica Cistern）。我在裡頭加了幾根從水裡伸出的柱子，貼上伊斯蘭風格的瓷磚圖案，天花板也做類似設計。牆壁則用了簡單的棋盤格圖案——這樣更能讓觀察者感受黑洞在視覺上造成的扭曲。我把黑洞懸浮在柱子間的半空。下方三張圖則分別顯示了「無陰影」、「只有陰影」、「完整渲染」三種狀態，強調在黑洞環境下正確處理陰影並不簡單，還有它獨特的光學效果。

在光線追蹤中，通常對陰影的處理方式是「找出物體與光源之間的直線」，再根據與光源的距離與角度來計算亮度。然而在黑洞時空中，1、找到一條能連結該物體到光源的光線本身就不簡單，2、而且往往不只一條，甚至可能是無限多條。為了因應這個複雜度，我採用了「非線性版的 Photon Mapping（光子映射）^[5]」，即從光源發出大量光子並記錄它們在場景中落點的位置。當我們要對某個表面進行著色時，只要看周圍落點的密集程度即可。如此就能避免像「計算所有可能光線」這種棘手問題。

Photon Mapping 有名的地方在於能逼真渲染「焦散（caustics）」，比如玻璃球或水面聚光處的高亮區域。我很早就想知道：「黑洞」可否也產生類似焦散？答案是肯定的——正如上面中圖與右圖看到的，黑洞上方的光源被其彎曲後，光子集中到黑洞正下方的水面上，形成一個亮點。這從下方兩張圖也更明顯：分別顯示有無黑洞時，光子在水面上落點的密度圖。

以下這段影片展示了該地下水窖場景：

正如前面提到的，想把以上場景變成全息圖，就必須從「黑箱」中抽絲剝繭。首先，我得把 Chimera 腳本移植到我的非線性光線追蹤程式裡；這並非最難的部分，難點反而在於了解「那些把圖像轉成全息圖的演算法是怎麼處理光線」的。由於目前大多數演算法都假定光線在「攝影機到全息平面」之間是直的，如果在這段區域內光線已經發生彎曲，就會破壞演算法。為了避免問題，只好讓黑洞座落在全息平面「後方」，在平面前方時光線還是沿直線走，穿過平面後再受到黑洞彎曲，如此折衷便能讓演算法繼續運行，同時也能保留黑洞在視覺上的扭曲效果。下圖說明這一點：

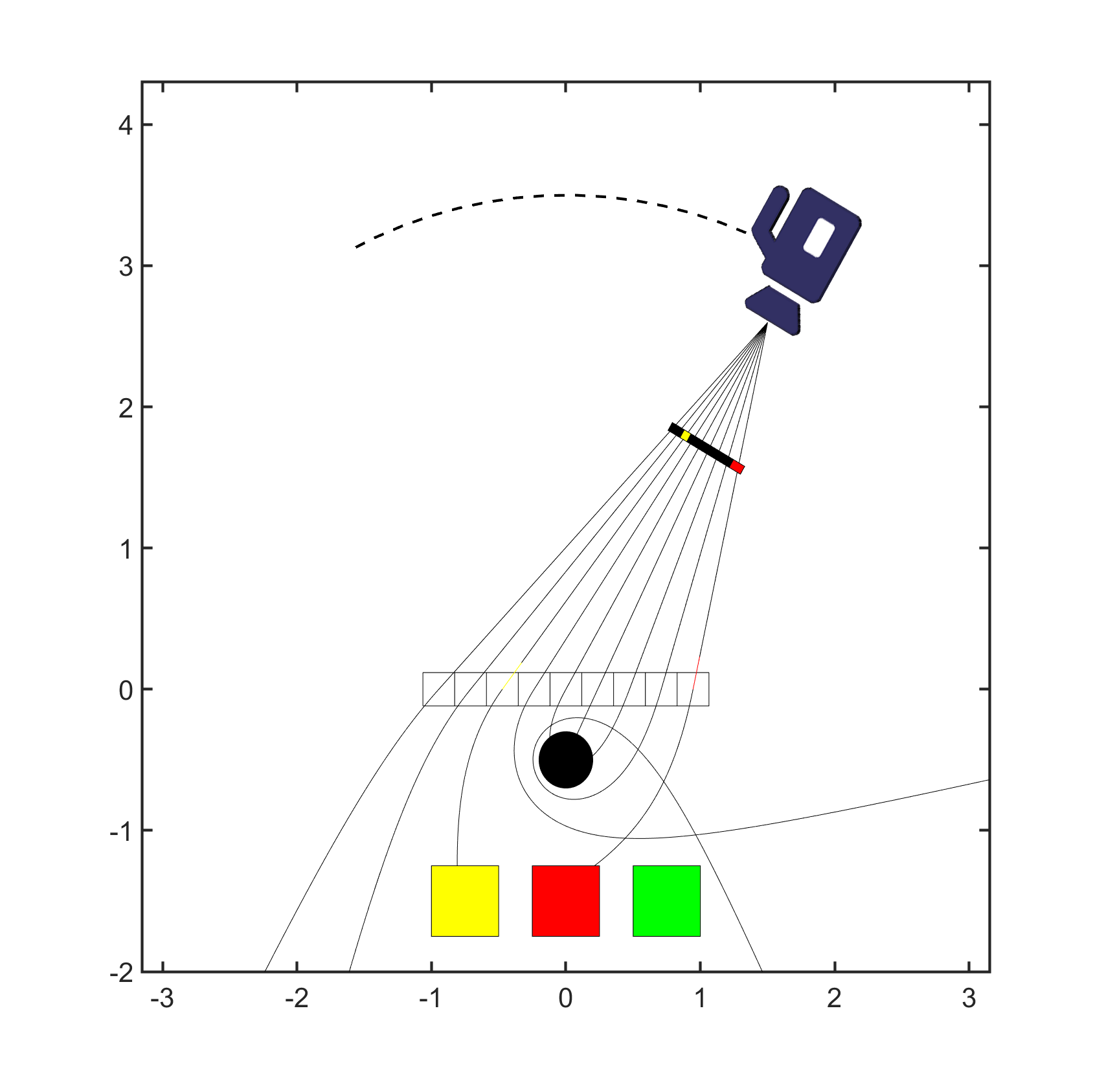
關於更多細節（以及最終全息圖的立體 3D 影片），可參考下方這段影片：

參考文獻

1. Luminet, J.-P. “Image of a spherical black hole with thin accretion disk.” Astronomy and Astrophysics, vol. 75, 1979, pp. 228–235.
2. Philippe Gentet and Seung-Hyun Lee. “True holographic ghost illusion.” Optics Express, Vol. 30, Issue 15, pp. 27531-27538 (2022)
3. Andrew J S Hamilton and Gavin Polhemus. “Stereoscopic visualization in curved spacetime: seeing deep inside a black hole.” New J. Phys., Vol. 12, 2010
4. Gröller, E. "Nonlinear ray tracing: Visualizing strange worlds." The Visual Computer 11, 263–274 (1995).
5. Jensen, H. "Realistic Image Synthesis Using Photon Mapping." 2001.